平衡树-1：从二叉查找树到平衡树

Splay和无旋Treap见第二篇文章

二叉查找树

BST 性质

二叉树有一种"堆性质"(每个节点的值大于或小于它的子节点的值)，现在介绍二叉树上的另一种性质，如下：

  • 当前节点的值大于等于其左子树上的任何节点
  • 当前节点的值小于等于其右子树上的任何节点
  • 左右子树均满足该性质

注意这里是"大于等于"与"小于等于"，不是严格大于或小于。

二叉查找树

查找

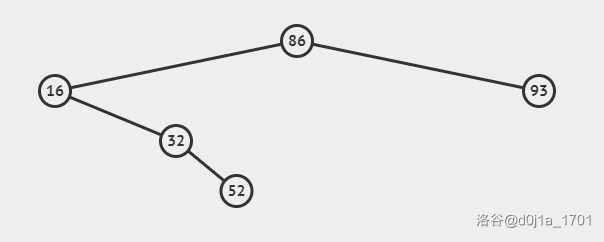
如图是一棵满足该性质的二叉树

所以这个性质有什么用呢？

在满足这个性质的二叉树上可以快速的查找某个节点:

比如在上面那张图中找 5252 我们的查找过程如下:

  1. 从根节点开始 86>5286 > 52 向左子树找
  2. 16<5216 < 52 向右子树找
  3. 32<5232 < 52 向右子树找
  4. 52=5252 = 52 找到了 返回结果

易得在满足此性质的二叉树中查找的时间复杂度取决于树高，在随机数据下期望树高为 O(log⁡n)O(\log n) ，所以查找的期望(记住这个期望)时间复杂度就是 O(log⁡n)O(\log n) 。由于优异的查找性能，这种二叉树被称为"二叉查找树"(Binary Search Tree,BST)，而这种性质则被称为"BST 性质"。

注意: 堆性质 和 BST性质 是目前关于二叉树最重要的两个性质

C++实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//基础声明 后文若无特殊声明均使用此段代码
//std=c++14
struct Node{
    int lc,rc,val;//左孩子，右孩子，值
}tree[10086];
int len,root;//用于创建节点
inline int newNode(int val){
    tree[++len] = {0,0,val};
    return len;
}

//BST-查找
int find(int id,int val){
    if(!id) return -1;//没找到返回-1
    if(tree[id].val > val)  return find(tree[id].lc,val);//查询左子树
    if(tree[id].val < val)  return find(tree[id].rc,val);//查询右子树
    return id;//如果不小于且不大于就必然等于 返回自身
}

插入

只有查找是不行的，还需要有插入操作

二叉查找树的插入也十分简单，只需要在查询时对查找路径上不存在的点执行插入操作。(为了简化操作先不考虑重复数据)

1
2
3
4
5
6
7
8
9
10
11
//BST-插入
void insert(int id,int val){//注意:此函数需要特判根节点是否为空
    if(tree[id].val > val){
        if(tree[id].lc) insert(tree[id].lc,val);//如果有左子树就递归
        else tree[id].lc = newNode(val);//否则左子树是一个新节点
    }
    if(tree[id].val < val){//同上
        if(tree[id].rc) insert(tree[id].rc,val);
        else tree[id].rc = newNode(val);
    }
}

可以使用引用简化代码(后文都将采用此写法)

1
2
3
4
5
6
7
8
9
int insert(int &id,int val){
    if(!id){
        id = newNode(val);//这里的id是引用，修改id就等于修改父节点的左孩子/右孩子
        return;
    }
    if(tree[id].val > val)  insert(tree[id].lc,val);//查询左子树
    if(tree[id].val < val)  insert(tree[id].rc,val);//查询右子树
    //如果执行到这一行说明重复插入
}

Q:为什么没有删除?

A:一般不直接使用BST而是使用平衡树(原因见下文)，而二叉查找树的删除极其难以实现(三种分类讨论)，一般直接使用平衡树的特性实现删除，故一般不需要学习BST的删除。

如果真的很想了解可以经典算法Baidu搜索深刻体会

例题

这些就是二叉查找树的基本操作了。运用BST性质你可以完成很多其他操作：

例题:luoguP5076 普通二叉树 简化版

BST 模板题，需要实现插入(insert)，查排名(rnk)，k 小值(kth)，前驱(pre)，后继(nxt)五种操作。

插入很简单，刚才学过。但是查排名 k 小值前驱后继怎么办？

这里的节点需要额外维护一个size域，表示以当前节点为根的子树大小。

并且注意这道题的value可重，于是直接开一个count域维护相同value的节点数量

所以节点声明的代码相应的变为

1
2
3
4
5
6
7
8
struct Node{
    int lc,rc,val,sz,cnt;//左孩子，右孩子，值，子树大小，数量
}tree[10086];
int root,len;
inline int newNode(int val){
    tree[++len] = {0,0,val,1,1};
    return len;
}

我们还需要一个pushup函数实现size域的更新。

1
2
3
inline void pushup(int id){
    tree[id].sz = tree[tree[id].lc].sz + tree[tree[id].rc].sz + tree[id].cnt;
}

插入代码变为:

1
2
3
4
5
6
7
8
9
10
void insert(int &id,int val){
    if(!id){
        id = newNode(val);
        return;
    }
    if(tree[id].val > val) insert(tree[id].lc,val);
    else if(tree[id].val < val) insert(tree[id].rc,val);
    else tree[id].cnt++;
    pushup(id);//别忘了pushup
}

根据BST性质和刚才我们维护的size域就可以实现其他操作了(自己去手推一下就明白了)。

查排名:

修改版的查找操作

1
2
3
4
5
6
int rnk(int id,int val){
    if(!id) return 1;
    if(tree[id].val > val)  return rnk(tree[id].lc,val);
    if(tree[id].val < val)  return rnk(tree[id].rc,val)+tree[id].sz-tree[tree[id].rc].sz;//如果val>当前节点上的值，说明val肯定比当前节点及它的左子树上的所有节点的值大
    return tree[tree[id].lc].sz + 1;//如果val=当前节点上的值，说明val肯定比它左子树上的所有节点的值大 注意排名的定义是比val小的数的个数+1
}

k 小值:

1
2
3
4
5
6
int kth(int id,int k){//别忘了排名(k)的意义是比val小的数的个数+1
    if(!id) return -1;//没找到
    if(k<=tree[tree[id].lc].sz)  return kth(tree[id].lc,k);//比当前节点小的数的个数(排名-1) >= k 找左子树
    else if(k<=tree[tree[id].lc].sz+tree[id].cnt)  return tree[id].val;//小于等于当前节点的数的个数 >= k 返回当前值
    return kth(tree[id].rc,k-tree[id].sz+tree[tree[id].rc].sz);//找右子树 k减去小于等于当前节点的数的个数
}

前驱&后继:

1
2
3
4
5
6
7
8
9
10
inline int pre(int val){
    int rk = rnk(root,val);
    if(rk==1)   return -2147483647;
    return kth(root,rk-1);
}
inline int nxt(int val){
    int x = kth(root,rnk(root,val+1));
    if(x==-1)   return 2147483647;
    return x;
}

完整版代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>
using namespace std;
struct Node{
    int lc,rc,val,sz,cnt;
}tree[10086];
int root,len;
inline int newNode(int val){
    tree[++len] = {0,0,val,1,1};
    return len;
}
inline void pushup(int id){
    tree[id].sz = tree[tree[id].lc].sz + tree[tree[id].rc].sz + tree[id].cnt;
}
void insert(int &id,int val){
    if(!id){
        id = newNode(val);
        return;
    }
    if(tree[id].val > val) insert(tree[id].lc,val);
    else if(tree[id].val < val) insert(tree[id].rc,val);
    else tree[id].cnt++;
    pushup(id);
}
int rnk(int id,int val){
    if(!id) return 1;
    if(tree[id].val > val)  return rnk(tree[id].lc,val);
    if(tree[id].val < val)  return rnk(tree[id].rc,val)+tree[id].sz-tree[tree[id].rc].sz;
    return tree[tree[id].lc].sz + 1;
}
int kth(int id,int k){
    if(!id) return -1;
    if(k<=tree[tree[id].lc].sz)  return kth(tree[id].lc,k);
    else if(k<=tree[tree[id].lc].sz+tree[id].cnt)  return tree[id].val;
    return kth(tree[id].rc,k-tree[id].sz+tree[tree[id].rc].sz);
}
inline int pre(int val){
    int rk = rnk(root,val);
    if(rk==1)   return -2147483647;
    return kth(root,rk-1);
}
inline int nxt(int val){
    int x = kth(root,rnk(root,val+1));
    if(x==-1)   return 2147483647;
    return x;
}
int q;
int main(){
	cin >> q;
	while(q--){
		int op,x;
		cin >> op >> x;
		switch(op){
			case 1:
				cout << rnk(root,x) << endl;
				break;
			case 2:
				cout << kth(root,x) << endl;
				break;
			case 3:
				cout << pre(x) << endl;
				break;
			case 4:
				cout << nxt(x) << endl;
				break;
			case 5:
				insert(root,x);
				break;
		}
	}
}

平衡树

关于 BST,它死了

前面说过，二叉查找树的时间复杂度取决于树高，然而这个树高虽然期望是 log⁡n\log n 级别 但是一旦遇到特殊构造的数据就会退化到 nn 级，然后得到 TLE\color{red}{\huge{\text{TLE}}} 。

"特殊构造数据"其实很简单，比如有序数据就可以卡掉不做优化的BST。

比如依次插入1,2,3,4,5,6,7,8，你就会得到这么个玩意:

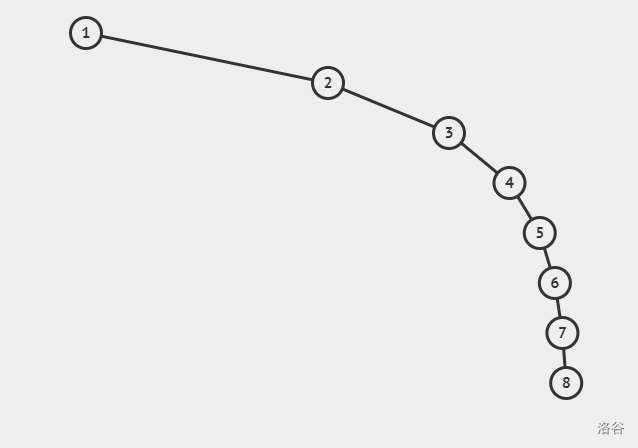
一叉查找链

可以发现二叉查找树退化成了一叉查找链链表，查询时间复杂度变成了惊人的 O(n)O(n) ！

我们肯定更希望自己的二叉查找树变成这样:

平衡树

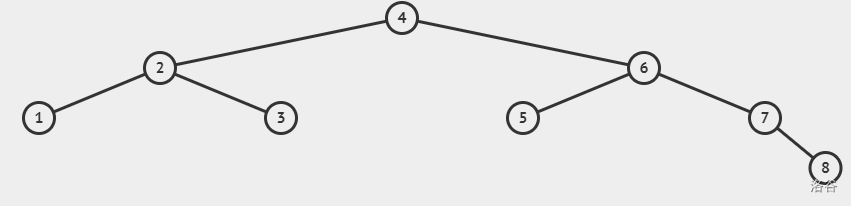
图二与图一的树的内容完全一样，但是图二所示的树的树高只有 log⁡n\log n 这正是我们希望看到的。从这里可以看出来，
对于相同的数据，二叉查找树可能有不同的结构。

我们希望有一种特殊的二叉查找树，它最好能够自动维持平衡，防止退化，这个时候就需要平衡树了。

旋转的二叉树

先介绍一下"旋转"操作，它能在不破坏BST性质的前提下交换当前节点与左孩子/右孩子。

左旋

右旋

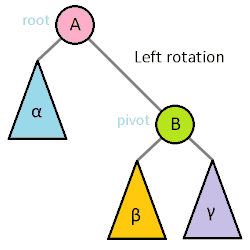
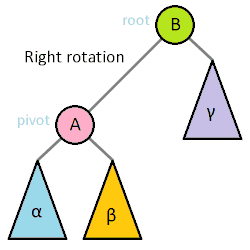
右旋可以将父节点与左孩子交换(然后本来的左孩子的右孩子变成了本来的父节点)，左旋可以将父节点与右孩子交换(然后本来的右孩子的左孩子变成了本来的父节点)。

一般将左旋称为zag，右旋称为zig。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void zig(int &id){//右旋
    int p = tree[id].lc;//待交换节点
    tree[id].lc = tree[p].rc;//第一步：待交换节点的右孩子挂到当前节点的左孩子上
    tree[p].rc = id;//第二步：当前节点挂到待交换节点的右孩子上
    tree[p].sz = tree[id].sz;//更新待交换节点的子树大小
    pushup(id);//更新当前节点的子树大小
    id = p;//第三步：当前节点父节点的孩子挂到待交换节点上（因为id是引用，修改id就等于直接修改当前节点父节点的孩子）
    //交换完成
}
void zag(int &id){//同理，不过要把lc和rc反过来
    int p = tree[id].rc;
    tree[id].rc = tree[p].lc;
    tree[p].lc = id;
    tree[p].sz = tree[id].sz;
    pushup(id);
    id = p;
}

Treap

不难发现，在随机数据下BST是趋近平衡的。但是作为一种在线数据结构，我们像不可能优化快排一样将输入数据随机打乱。

可以考虑在每个节点上新增一个weight域，每次新建节点时将weight域赋值为随机数。

1
2
3
4
5
6
7
8
9
struct Node{
    int lc,rc,val,sz,cnt,w;
}tree[100010];
int root,len;
mt19937 mt(chrono::system_clock::to_time_t(chrono::system_clock::now()));//C++11 高性能随机数生成器 #include <random> & #include <chrono>
inline int newNode(int val){
    tree[++len] = {0,0,val,1,1,(int)mt()};//w为随机数
    return len;
}

然后呢？为了随机打乱这棵树，我们可以用weight域建一个堆。

堆的插入需要交换节点，还记得上面提到的旋转吗？

旋转操作可以交换父子节点，这样就可以维护堆性质了！把大根堆和BST进行结合，我们就得到了树堆(Treap,Tree+Heap=Treap)。

插入

先复习一下大根堆的插入：在最后一个节点后插入，如果当前节点值小于父节点值则交换。把它放到二叉查找树的插入里：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void insert(int &id,int val){
    if(!id){
        id = newNode(val);
        return;
    }
    tree[id].sz++;//因为插入必定成功，所以路径上的每一个点都要更新(不用写pushup了)
    if(tree[id].val > val){
        insert(tree[id].lc,val);
        if(tree[tree[id].lc].w > tree[id].w)    zig(id);//如果父节点的w大于子节点就交换
    }else if(tree[id].val < val){
        insert(tree[id].rc,val);
        if(tree[tree[id].rc].w > tree[id].w)    zag(id);
    }else tree[id].cnt++;//重复节点
}

删除

本来这个东西非常麻烦，需要三个分类讨论，但是我们现在有了旋转 (然而还是很麻烦) 。直接把待删除的节点转到叶子节点(或只有一个子节点的节点)然后直接删除即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void erase(int &id,int val){
    if(!id) return;
    if(tree[id].val==val){//找到了就开始删
        if(tree[id].cnt>1){
			tree[id].cnt--;
			pushup(id);//千万不要忘了这个pushup! 每次写return前最好都检查一下
			return;
		}else{
            if(!tree[id].lc||!tree[id].rc)    id = tree[id].lc + tree[id].rc;//如果只有一个子节点或没有子节点就直接删除
            else if(tree[tree[id].lc].w > tree[tree[id].rc].w)    zig(id),erase(tree[id].rc,val);
            else zag(id),erase(tree[id].lc,val);//如果有两个子节点把那个较小的旋上来然后向另一边递归
        }
    }else if(tree[id].val > val)    erase(tree[id].lc,val);//标准的BST上查找
    else	erase(tree[id].rc,val);
    pushup(id);//别忘了更新size域
}

由于Treap同时满足堆性质和 BST 性质，所以其他操作直接复制 BST 的就行。

例题

例题:luoguP3369 模板:普通平衡树

和上面那个普通二叉树基本上一样，只是增强了数据，多了删除操作，还改了下操作编号。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include <iostream>
#include <random>
#include <chrono>
using namespace std;
struct Node{
    int lc,rc,val,sz,cnt,w;
}tree[100010];
int root,len;
mt19937 mt(chrono::system_clock::to_time_t(chrono::system_clock::now()));
inline int newNode(int val){
    tree[++len] = {0,0,val,1,1,(int)mt()};
    return len;
}
inline void pushup(int id){
    tree[id].sz = tree[tree[id].lc].sz + tree[tree[id].rc].sz + tree[id].cnt;
}
void zig(int &id){
    int p = tree[id].lc;
    tree[id].lc = tree[p].rc;
    tree[p].rc = id;
    tree[p].sz = tree[id].sz;
    pushup(id);
    id = p;
}
void zag(int &id){
    int p = tree[id].rc;
    tree[id].rc = tree[p].lc;
    tree[p].lc = id;
    tree[p].sz = tree[id].sz;
    pushup(id);
    id = p;
}
void insert(int &id,int val){
    if(!id){
        id = newNode(val);
        return;
    }
    tree[id].sz++;
    if(tree[id].val > val){
        insert(tree[id].lc,val);
        if(tree[tree[id].lc].w > tree[id].w)    zig(id);
    }else if(tree[id].val < val){
        insert(tree[id].rc,val);
        if(tree[tree[id].rc].w > tree[id].w)    zag(id);
    }else tree[id].cnt++;
}
void erase(int &id,int val){
    if(!id) return;
    if(tree[id].val==val){
        if(tree[id].cnt>1){
			tree[id].cnt--;
			pushup(id);
			return;
		}else{
            if(!tree[id].lc||!tree[id].rc)    id = tree[id].lc + tree[id].rc;
            else if(tree[tree[id].lc].w > tree[tree[id].rc].w)    zig(id),erase(tree[id].rc,val);
            else zag(id),erase(tree[id].lc,val);
        }
    }else if(tree[id].val > val)    erase(tree[id].lc,val);
    else	erase(tree[id].rc,val);
    pushup(id);
}
int rnk(int id,int val){
    if(!id) return 1;
    if(tree[id].val > val)  return rnk(tree[id].lc,val);
    if(tree[id].val < val)  return rnk(tree[id].rc,val)+tree[id].sz-tree[tree[id].rc].sz;
    return tree[tree[id].lc].sz + 1;
}
int kth(int id,int k){
    if(!id) return -1;
    if(k<=tree[tree[id].lc].sz)  return kth(tree[id].lc,k);
    else if(k<=tree[tree[id].lc].sz+tree[id].cnt)  return tree[id].val;
    return kth(tree[id].rc,k-tree[id].sz+tree[tree[id].rc].sz);
}
inline int pre(int val){
    int rk = rnk(root,val);
    if(rk==1)   return -2147483647;
    return kth(root,rk-1);
}
inline int nxt(int val){
    int x = kth(root,rnk(root,val+1));
    if(x==-1)   return 2147483647;
    return x;
}
int q;
int main(){
	cin >> q;
	while(q--){
		int op,x;
		cin >> op >> x;
		switch(op){
			case 1:
				insert(root,x);
				break;
			case 2:
				erase(root,x);
				break;
			case 3:
				cout << rnk(root,x) << endl;
				break;
			case 4:
				cout << kth(root,x) << endl;
				break;
			case 5:
				cout << pre(x) << endl;
				break;
			case 6:
				cout << nxt(x) << endl;
				break;
		}
	}
}
数据结构
#二叉查找树 #BST #平衡树 #Treap #数据结构 #讲义
平衡树-1：从二叉查找树到平衡树
https://blog.ikale.io/p/87d2831a/
作者
Ikaleio
发布于
2021年8月13日
许可协议
CC-BY-SA