ST表学习笔记

RMQ

简介

区间最值问题(Range Maximum/Minimum Query,RMQ)是一类经典的区间问题，其一般形式如下：

给定一个 $n$ 个元素的数组 $arr$ ，给定 $m$ 个形式为 $l_i,r_i$ 的询问，对于每个询问 $i$ 求 $max\{arr_{l_i},arr_{l_{i+2}},arr_{l_{i+3}}...,arr_{r_i}\}$

显然这种问题可以被线段树以每次询问 $O(\log n)$ 的时间复杂度轻松解决，但是线段树的常数较大，有时会超时。

ST 表

ST 表(Sparse Table,ST,又名稀疏表)可以在进行 $O(n \log n)$ 的预处理后用 $O(1)$ 的时间复杂度处理每次 RMQ(或者其他任何满足可重复贡献和结合律的操作，比如区间gcd)的询问，但前提是无修改操作。

原理

什么是可重复贡献问题？

可重复贡献问题 是指对于运算 $opt$，满足 $x\space opt\space x = x$，则对应的区间询问就是一个可重复贡献问题。例如，最大值有 $max(x,x) = x$，gcd 有 $gcd(x,x) = x$，所以 RMQ 和区间 GCD 就是一个可重复贡献问题。像区间和就不具有这个性质，如果求区间和的时候采用的预处理区间重叠了，则会导致重叠部分被计算两次，这是我们所不愿意看到的。另外， 还必须满足结合律才能使用 ST 表求解。

摘自 OI-Wiki

ST 表通过倍增思想实现。

对于区间最大值问题， $st_{i,j}$ 代表从 $j$ 开始 $2^i$ 个数的最大值（其他操作同理，下文均以区间最大值举例）。

为什么 $2^i$ 那维要放在前面？

这样能保证程序中内存访问的连续性，增加运行速度（每日一个卡常小技巧）。

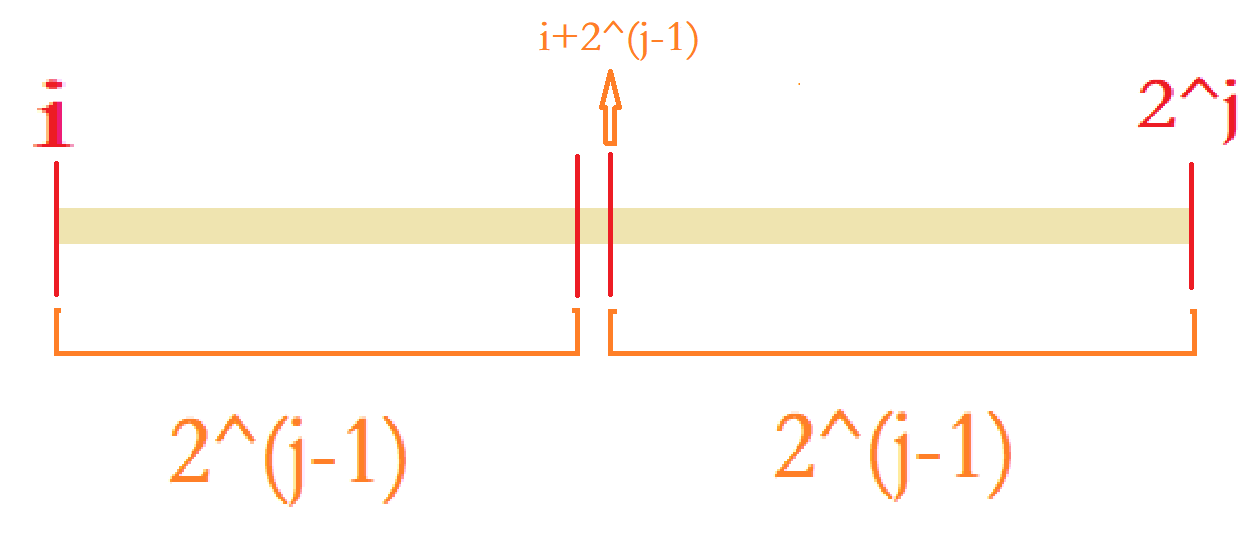
建表

ST 表的建表也很好写，根据图片看出， $st_{i,j} = max\{st_{i-1,j},st_{i-1,j+2^{i-1}}\}$

inline void build() {
	for(int i = 1; i <= lg[n]; i++)
		for(int j = 1; j + (1 << i) - 1 <= n; j++)
			st[i][j] = max(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
}

查询

根据"可重复贡献"，查询时区间的重复是不影响结果的，所以我们可以写出查询的代码：

inline int query(int l, int r) {
	int k = lg[r - l + 1];
	return max(st[k][l], st[k][r - (1 << k) + 1]);
}